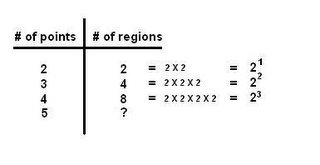late post? yes, i know... IM REALLY SORRY =(
hmm what happened in class yesterday?
okay,when we got to class Mr. K asked us to draw a BIG circle on a piece of paper. Before we started our activity he mentioned that "Math is science of patterns".
Then Mr. K started off by asking us... "If we connect two points (along the circumference of the circle) how many regions will the circle be divided into ?"
We all know that if we connect two points then it will be divided into 2 regions.
"how about 3 points connected all together?"
he drew on the board three points along the circumference of a circle then counted the number of regions. 4 regions.
and then he asked us to choose 4 points along the circumference of the circle, connect it and count how many regions the circle was divided into. 8 regions.
then we made a chart that looked like this:

looking at the table/chart, is there a pattern? yes there is..
what is the pattern? the number of regions goes up by multiplying 2 to it.
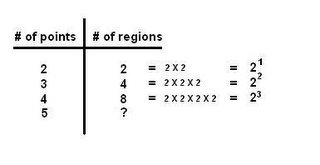
then Mr. K asked us to guess what the next number would be.
"16" the students answered...
is that correct?
well, we have to check if it is...so we drew 5 points along the circumference of the circle and counted the number of regions.
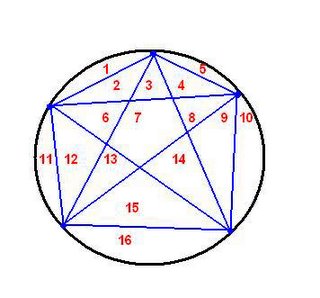
16! we were right !
Then Mr. K asked if the number of points was "n", can we come up with a formula for it?
one of the students said " if n represents the number of points then the number of regions will be 2n-1.
why "n-1"?
n-1 because the exponent of the number of regions is always one less than the number of points.
Then Mr. K asked what if we have 6 points connected all together? how many regions will the circle be divided into?
using the formula : 26-1 or 25 we got 32.
and just like before we have to check... so we drew a circle with 6 points connected to each other then counted the regions.
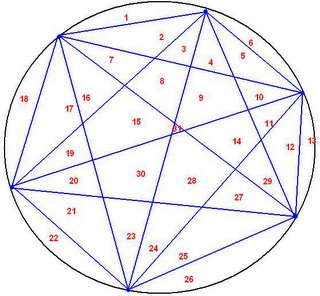
31 regions ?! only 31. That means that the formula we came up with is not true and must be discarded.(some may have gotten only 30 regions. why? maybe you just missed counting a little region or you drew your circle too many) notice that there`s a little triangle region in the middle of the above diagram? if you drew your circle big enough then it should show.

Therefore 6 is the counter example for the formula 2n-1.
coun·ter·ex·am·ple;
-an example that disproves a hypothesis, proposition and/or theorem.
"PRIME PRODUCING" POLYNOMIAL
F(x)=x2+x+41
is this really a prime producing formula? let`s check it out.
F(1) = 43 prime
F(2) = 47 prime
F(3) = 53 prime
F(4) = 61 prime
F(5) = 71 prime
okay, so far all the result are prime numbers but is it right to conclude that f(x) will be prime for ALL intergers?
answer: NO
why?: because if you try to solve it with x = 40
F(4o)=4o2+4o+41
F(40)=40(40+1)+41
F(40)=1681 which is also 412
MARIN MERSENNE.

(picture taken from:http://shl.stanford.edu/Eyes/kircher/mersenne.html)
Marin Mersenne is a french theologian, natural philosopher, and mathematician who tried to find a formula that would represent all primes but didn't succeed. Although he failed, his work on numbers of the form
2p - 1
p prime
is still of interest in the investigation of large primes.
He's name is best remembered today for Mersenne Prime.
Mersanne Prime: are primes of the form 2p-1.
For more about Mersanne Primes: *click_here* or here
(it includes a table of known Mersenne Primes, who discovered it and when)
So far they have only found 42? mersenne primes.
Wanna become world famous? or even win some cash? You can participate in what they call GIMPS. Great Internet Mersenne Prime Search. They have already found seven of them on GIMPS.
If you're interested you can CLICK_HERE. It tells you how it works, how long it will take, how much you can win, what you need to have, EVERYTHING you need to know. :)
for more about Marin Mersanne clickhere
VENN DIAGRAMS
Mr. K also posted up some questions on the board.
1.) In a group of students 12 are taking chemistry, 10 are taking physics, 3 are taking both and 5 are taking neither. How many students are in the group?
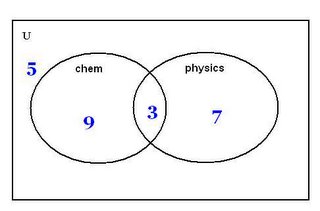
ANSWER: 24 students are in the group
2.)In a third-rate rock band, 3 people play guitar, 4 sing, 2 do both and 6 have no talent for singing or guitar so they do something else. How many are in the band?
ANSWER:There are 11 people in the band.
3.)There are 64 kids in the "Tiny Little Cherubs"(TLC) Daycare. At lunch 59 ate green beans, 56 cauliflower, 60 ate brocolli, 55 ate green beans and cauliflower, 54 cauliflower and brocolli, 56 green beans and brocolli and 53 ate all. How many ate none?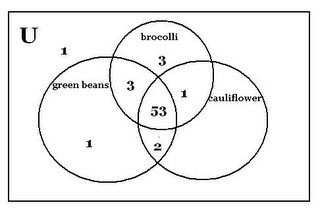
ANSWER: One kid ate none.
OKAY... maybe i exaggerated when i said it wasnt half way yet -_-". lol. hhm, thats all i could remember...so i guess this is it.
THE EEND :)
sorry again for being late!
*if i missed anything please let me know*
oh and i found a cool site about prime puzzles and problem connected. I don't have a delicious account so i guess ill just link it in here.
primepuzzles
There's a new puzzle every saturday and the solutions will be up one week later.
oh... the scribe today was jamilynG. check out her scribe post for tomorrow's scribe.