scribblin' scribe....
2. Write two equations ( Sine, Cosine) for this graph. 
Today we worked on some problems on the board. Here they are:
1. Graph y = -2cos(x+45)+3
A = 2
B = 1 <<>
C = 45
D = 3
Y = A sin B (X-C) + D
Y = 2 sin (X-45) + 3 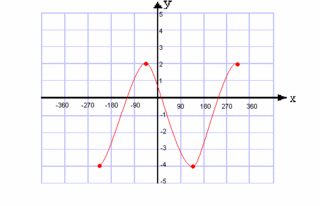
Y = A sin B (X-C) + D
A = 3
B = 1
C = -135 / 45
D = -1
Y = 3 sin (x+135) - 1
Y = -3 sin (x-45) - 1
Y = A cos B (X-C) + D
A = 3 Y = 3 cos (X+45) - 1
B = 1 Y = -3 cos (X-135) - 1
C = -45 / 135
D = -1
3. A car is driving due east along a road. The driver sees a radio tower in the direction N56'E and 5280m away. The radio tower had a range of 3500m.
a) How much farther must she drive to get "in range" of the radio.
b) For what length of the road (distance) will she be able to listen to this radio station.
Sin34/3500 = Sin*/5280 = .8436 = 57.5' or 122.5' Since we are smarter then the average bear we know that the obtuse angle Now we solve with the sine law. Sin88.5/X=Sin34/3500 = 6256.9m <> Sin65/x=Sin57.5/3500 = 3761.1m <> 6256.9 - 3761.1 = 2495.8m a) She needs to travel 2495.8m more to be in range. b) Once she starts in range she will travel 3761.1m until she will travel out of range. 4. An 11cm long line is drawn at an angle of 44' to a horizontal line AB. A circle with centre C and radius 9cm is drawn cutting the horizontal line at points C&D. Find the length of CD. We know the obtuse angle is 121.9' and the acute angle is 58.1'. Sin61.9/x = Sin 58.1'/9 CD = 9sin61.9'/sin58.1 = 9.4cm 5. A golfer takes two putts to get the golf ball into the hole. The first putt rolls the ball 10.2m in the northwest direction, and the second putt sends the ball due north 3.7m into the hole. How far & in what direction should the golfer have aimed in the first putt to get a "hole in one"? I don't know how to square do this a*2 will mean a-squared =). a*2 = b*2 + c*2 - 2 b c cosA a*2 = 3.7*2 + 10.2*2 - 2 (3.7) (10.2) cos135' a*2 = 171.1 square root it = 13.1m To find what angle he should've hit it in... SINE LAW Sin135/13.1=Sin*/3.7m = .1997 11.5' +45' = 56.5' away from the x=axis. Well you guys might want to check my math becuase I'm not too sure about myself. REMINDER pre-test tomorrow with subsitute so study study study!!! Sorry it took so long I didn't realize the pictures were so hard to make. TEST ON WEDNESDAY DO NOT MISS! COME PREPARED! Welll I guess that's it.... good luck everybody and before I forget next scribe is....... RoselS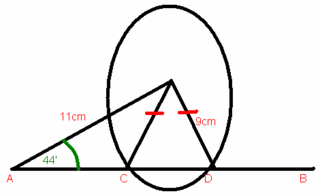
Sin44'/9 = Sin*/11 = 0.8490 = 58.1' and 121.9'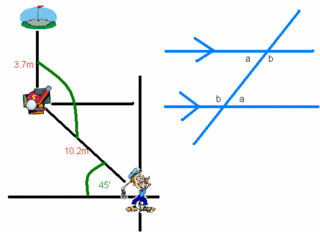 To solve this problem we'll have to do cosine law.
To solve this problem we'll have to do cosine law.




1 Comments:
Very Excellent. You Put Colours to show what's important and you had crazy Diagrams.
Post a Comment
<< Home