Man...
You had to pick me...
Man...
... ... ...
Man...
Sigh///
Ok. Fine...
Ok now that thats over with.
Today in class I get randomly chosen as scribe by Rannell. Thanks...
So anyways. First we had to do three questions like what we usually do.
USE THE QUADRATIC FORMULA TO FIND THE ROOTS
If any of you forgot what the Quadratic Formula was...
Sing the Song. lol
a) f (x) = 2x2 - 3x - 4
b) f (x) = - 2x2 + 3x + 1
c) f (x) = x2- 6x + 10
Answer to A)

Answer to B)
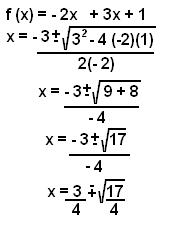
Then Mr. K. Told us why it's negative over positve.
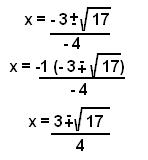
Answer to C)

Then we went back to factor trees. lol.
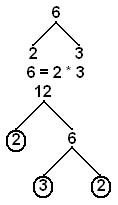
Fundamental Therom of Arithmetic. Only 12 can have the number 2,2,3.
We learned about a German Mathematician named GODEL.
He proved that certain things we know can be true but we dont actually know it's true.
For Example.
This Sentence is False.
He invented the GODEL number.
5 = 20*30*51
Fundamental Therom of Algebra
Any polynomial, whatever it is, it has to have the roots equal to the degree of the polynomial.
For example
f (x) = (x - 3)2
= (x - 3)(x - 3)
Then we learned that Some Roots can be imaginary. I'm like what...
Then we learned about a Swiss Mathematician called EULER and that he's responsible for PIE and E which is actually 2.17817... etc.
I wonder if Mr. K has a piece of E???
Hm...
Anyways then we get this whole explanation on how there are imaginary numbers outside the real numbers and stuff.
AKA It leads to this...
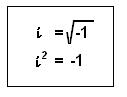
And This...
Some examples...
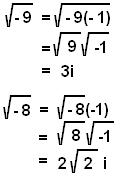
Then we finish question C. In the "Complex number system"
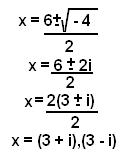
Then we learned about The Discriminant
b2 - 4ac <' 0
No Real Roots
(2 Complex or Imaginary Roots)
b2 - 4ac = 0
One Real Root
b2 - 4ac > 0
2 Real Roots
Then we get some notes in our Dictionary... I'll get Graeme to fill you in next time he has some notes. lol.
Mr. K. Then went over some question's on Exercise 14 & 15. Provided by Robert.
Homework if you didn't do it is Exercise 16 but leave out Questions 10, 11, 12, 13
Tomarrow we have a sub. Mr. Clark.
AND THE SCRIBE FOR TOMARROW IS... KAT L.






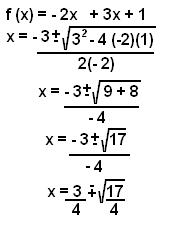
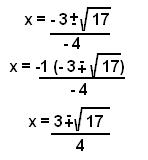


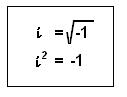

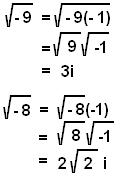
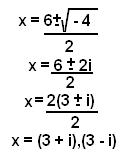

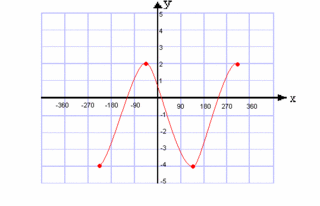
 Today I emphasized how to solve equations and trig equations by "recognizing the quadratic pattern". You can find a review of factoring
Today I emphasized how to solve equations and trig equations by "recognizing the quadratic pattern". You can find a review of factoring 



 Test day is Wednesday. I'm away for the next two days. Use the comments of this post to share with Mr. Tram, my substitute, your personal "Muddiest Point". You can use your name or leave your comment anonymously, but, whatever you do, share your troubles here. Remember, not only can Mr. Tram help you but you can help each other too! Leave tips and advice in the comments for your classmates. And don't forget, you can form an online study group and "meet" in the chatbox of our blog! Unlike Sysiphus, you're being set up to succeed! Take advantage of every opportunity you've got!
Test day is Wednesday. I'm away for the next two days. Use the comments of this post to share with Mr. Tram, my substitute, your personal "Muddiest Point". You can use your name or leave your comment anonymously, but, whatever you do, share your troubles here. Remember, not only can Mr. Tram help you but you can help each other too! Leave tips and advice in the comments for your classmates. And don't forget, you can form an online study group and "meet" in the chatbox of our blog! Unlike Sysiphus, you're being set up to succeed! Take advantage of every opportunity you've got!



